

- 생각
octorbirth.tistory.com/243여기를 통해 이해하였다.
2 * N 직사각형이 주어질 때, 2×1과 2×2 타일로 채우는 방법의 수
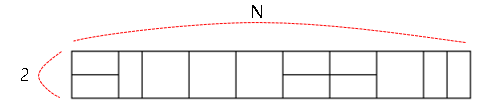
[구현]
Dynamic Programming (DP) 이용.
▶ DP[i] = 2 * i 직사각형에서 방법의 수

3 ≤ i 일 때, DP[i]는 DP[I-1]에서 크기 『1』만큼 늘어났기에
□ 을 놓는 경우입니다.

① DP[i-1]에서 2*1 크기의 □을 놓는 경우입니다.
■ 영역은 작은 단계에서 부터 쌓여온것이기 때문에 어떤 형태든 신경쓰지 않습니다.

② DP[i-2]에서 2*2 크기의 □ 1개 or 2*1 크기의 □를 2개 놓는 경우입니다.
→ DP[i-2] * 2

▶ DP[i] = DP[i-1] + (DP[i-2] × 2)
※ 0 ≤ n ≤ 250이기 때문에 Java의 경우 BigInteger 이용.
※ 문제 조건상 i = 0일 때, DP[0] = 0도 정의
- 코드
정답 코드 : 점화식으로 구현하였다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.math.BigInteger;
import java.util.Scanner;
import java.util.StringTokenizer;
public class Main {
static StringBuilder sb;
static BigInteger[] dp;
public static void main(String[] args) throws Exception {
SetData();
System.out.println(sb);
}
private static void SetData() throws Exception {
Scanner sc = new Scanner(System.in);
dp = new BigInteger[251];
sb = new StringBuilder();
dp[0] = new BigInteger("1");
dp[1] = new BigInteger("1");
dp[2] = new BigInteger("3");
for(int i=3; i<=250; i++) {
dp[i] = dp[i-2].multiply(new BigInteger("2"));
dp[i] = dp[i].add(dp[i-1]);
}
while(sc.hasNextInt()){
int n = Integer.parseInt(sc.next());
sb.append(dp[n] + "\n");
}
}
}'algorithm' 카테고리의 다른 글
| [JAVA] 백준 2294번 : 동전 2 (0) | 2020.12.21 |
|---|---|
| [JAVA] 백준 2981번 : 검문 (0) | 2020.12.21 |
| [JAVA] 백준 11058번 : 크리보드 (0) | 2020.12.18 |
| [JAVA] 백준 11047번 : 동전 0 (0) | 2020.12.17 |
| [JAVA] 백준 16120번 : PPAP (0) | 2020.12.17 |